Online Demo About Downloads Publications Case Studies

The Grade Protocol

Background

Assume that a group of students has been graded and would like to find out the sum of all their grades, e.g. to compute the average. However, none wants to reveal their individual grade in the process. The task can be accomplished with the following randomised algorithm. Let S ∈ N be the number of students, and let {0, · · · , G − 1} (G ∈ N) be the set of grades. Define N = (G − 1) · S + 1. Further we assume that the students are arranged in a ring and that each pair of adjacent students shares a random integer between 0 and N − 1. Thus a student shares a number l with the student on the left and a number r with the student on the right, respectively. Denoting the student’s grade by g, the student announces the number (g + l − r) mod N . Because of the ring structure, each number will be reported twice, once as l and once as r, so the sum of all announcements (modulo N ) will be the same as the sum of all grades.

Anonymity of the grades

What we can verify is that only this sum can be gleaned from the announcements by a casual observer, i.e. the observer cannot gain access to any extra information about individual grades. This correctness condition can be formalised by a specification, in which the students make random announcements subject to the condition that their sum equals the sum of their grades. Correct protocol. To check correctness of the Grade protocol, we check if the automaton resulting from the implementation of the protocol is equivalent to the specification automaton. Both automata are presented in Figure 5 for G = 2 and S = 3. Both automata accept words which are sequences of grades and announcements. The words are accepted with the same probability as that of producing the announcements for the given grades. Adherence to specification can then be verified via language equivalence. In Figure 6 we report various data related to the performance of apex and the equivalence checking algorithms. The reported times tspec and tprot are those needed to construct the automata corresponding to specification and the pro- tocol respectively (we also give their sizes sspec , sprot ). The columns labelled by t_←,rand , t_←,det, t_→,rand, t_→,det give the running time of the language equivalence check of the respective automata using the four algorithms. The symbol − means that the computation timed out after 10 minutes. The running time of the deterministic backwards algorithm is higher than the one of the forward algorithm because the backwards algorithm constructs a different vector space with a higher number of dimensions.

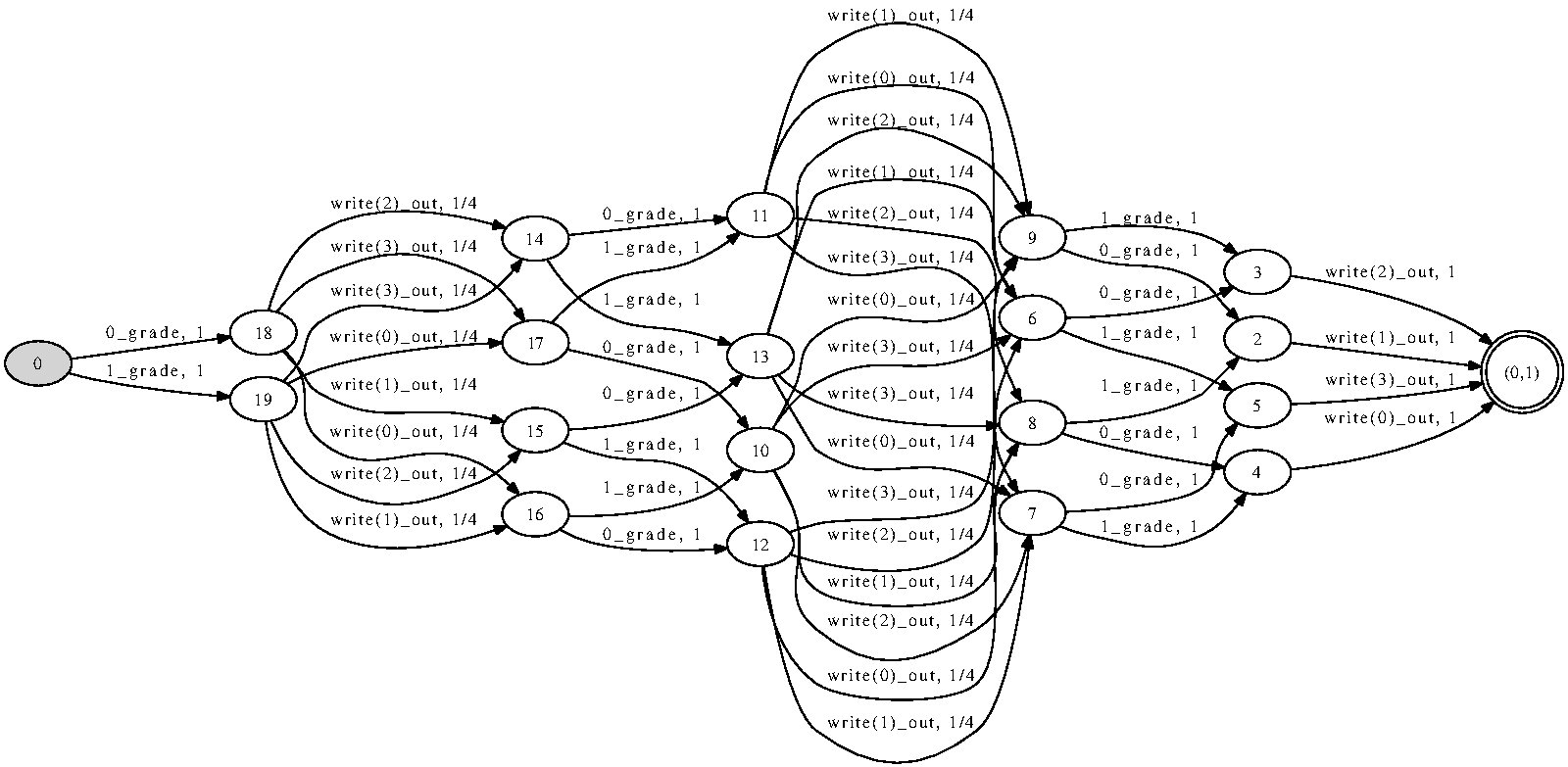
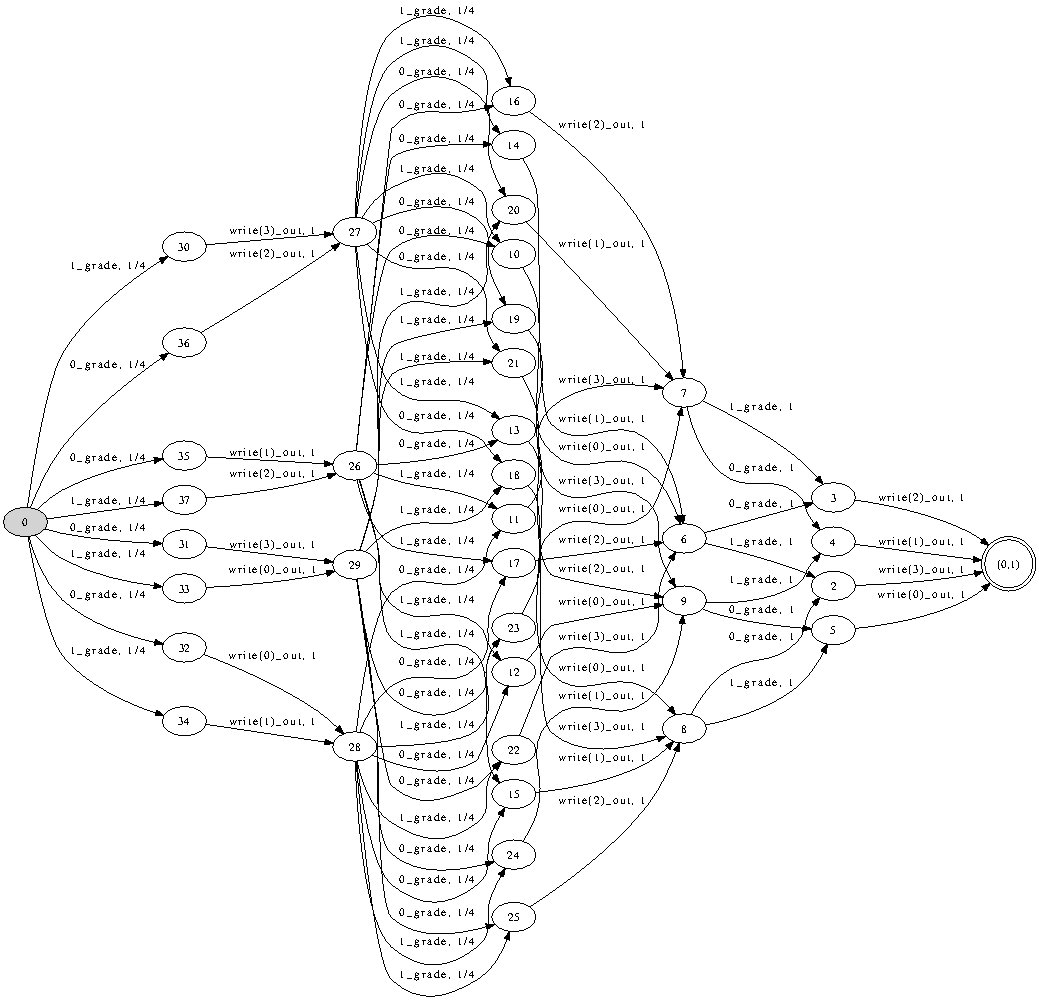
// PRINTS OUT PAIRS (GRADE,ANNOUNCEMENT)
// ANONYMITY CAN BE VERIFIED BY CHECKING
// LANGUAGE EQUIVALENCE WITH SPECIFICATION (grade-spec.txt)

// number of students
//const STUDENTS:= 3;

// grades: 0,1,...,GRADES-1
//const GRADES:=2;

const N := STUDENTS*(GRADES-1)+1;

grade:int%GRADES, out:var%N |-
		     var%(STUDENTS+1) i;

		    var%N first;
                    first:=rand[N];

                    var%N right;
                    right:=first;

                    i:=0;
		    while(i<STUDENTS) do { 
                                         var%N left;
                                         i:=succ(i); 
                                         left :=  if (i=STUDENTS) then first else rand[N];
		                         out := (grade + left) - right;
                                         right := left;
                                         }
:com

// SPECIFICATION TO BE USED WITH grade-impl2.txt

//const STUDENTS:=10;
//const GRADES:=10;

const N := STUDENTS * (GRADES-1) + 1;

grade:int%GRADES, out:var%N |-

		    var%STUDENTS i;
		    var%N total;

                    i:=1;
		    while(i) do { 
                                         total := grade + total;
                                         var%N r;
                                         r := rand[N]; 
                                         out:=r;
                                         total := total - r;
                                         i:=succ(i)
                                };

                    out:= grade + total: com

G	S	t_spec	t_prot	s_spec	s_prot	t_←,rand	t_←,det	t_←,rand	t_←,det

2	10	0.00	0.02	202	1102	0.00	0.41	0.00	0.02
2	20	0.05	0.24	802	8402	0.10	26.09	0.03	0.26
2	50	1.75	6.46	5,002	127,502	8.08		1.21	10.07
2	100	25.36	82.26	20,002	1,010,002	240.97		10.56	159.39
2	200	396.55		80,002

3	10	0.02	0.16	383	3803	0.02	5.79	0.01	0.09
3	20	0.22	1.64	1,563	31,203	0.69	598.78	0.23	1.33
3	50	6.99	39.27	9,903	495,003	61.76		9.29	63.16
3	100	102.42	39,803
3	200

4	10	0.04	0.56	564	8124	0.07	37.32	0.04	0.36
4	20	0.53	5.47	2,324	68,444	2.25		0.77	4.95
4	50	15.94	142.59	14,804	1,102,604	210.00		30.27	222.50
4	100	232.07		59,604
4	200

5	10	0.09	1.46	745	14,065	0.17	164.87	0.10	0.68
5	20	0.96	16.39	3,085	120,125	5.36		1.92	14.49
5	50	28.81	417.58	19,705	1,950,305	508.86		62.64	335.01
5	100	100	417.59		79,405
5	200

|| Specification automaton ||

|| Implementation automaton||

Faulty protocol

Moving to test cases for inequivalence checking, we compare the specification for the Grade Protocol with a faulty version of the protocol in which the students draw numbers between 0 and N − 2 (rather than N − 1, as in the original protocol). The running times and automata sizes are recorded in Figure 7. Both the deterministic and the randomised algorithms are decision algorithms for equivalence and can also generate counterexamples, which could serve, e.g., to repair a faulty protocol. We test counterexample generation on the faulty version of the protocol. The deterministic algorithm stores words in the work list which immediately yield a counterexample in case of inequivalence. In the context of the randomised algorithm (as described in Section 2.4), counterexample generation requires extra work: words need to be reconstructed using matrix vector multiplications. To quantify the runtime overhead, we record running times with counterexample generation switched on and off. The running time of the backward randomised algorithm with counterexample generation is denoted by t_←,rand and analogously for the forward algorithm. The runtime overhead of counterexample generation remains below 12%.

Imprint/Impressum Data Protection/Datenschutzhinweis