Anonymity is a key concept in computer security. It arises in a wide range of contexts, such as voting, blogging, making donations, passing on sensitive information, etc. A celebrated toy example illustrating anonymity is that of the ‘Dining Cryptographers protocol’ [ Chaum 1988 ]. Imagine that a certain number of cryptographers are sharing a meal at a restaurant around a circular table. As the end of the meal, the waiter announces that the bill has already been paid. The cryptographers conclude that it is either one of them who has paid, or the organisation that employs them. They resolve to determine which of the two alternatives is the case, with the proviso that for the former the identity of the payer should remain secret.

A possible solution goes as follows. A coin is placed between each pair of adjacent cryptographers. The cryptographers flip the coins and record the outcomes for the two coins that they can see, i.e., the ones that are to their immediate left and right. Each cryptographer then announces whether the two outcomes agree or disagree, except that the payer (if there is one) says the opposite. When all cryptographers have spoken, they count the number of disagrees. If that number is odd, then one of them has paid, and otherwise, their organisation has paid. Moreover, if the payer is one of the cryptographers, then no other cryptographer is able to deduce who it is.

There are many formalisations of the concept of anonymity in the literature. The earliest approaches ignored probabilities and relied instead on nondeterminism; anonymity was then equated with ‘confusion’, or more precisely with notions of equivalence between certain processes [ Schneider, Sidiropoulos 1996 ]. For example, in the case of the dining cryptographers, every possible behaviour visible to one of the cryptographers (i.e., outcomes of the two adjacent coin flips and subsequent round of announcements) should be consistent with any of the other cryptographers having paid, provided the number of disagrees is odd. A more sophisticated treatment takes probabilities into account. In our example, assuming the coins are fair, it can be shown that the a posteriori probability of having paid, given a particular protocol run, is the same for all cryptographers. Note that this does not hold if the coins are biased, which highlights one of the advantages of using probability over nondeterminism. A survey of the literature, as well as an in-depth treatment using process algebra, can be found in [ Bhargava, Palamidessi 2005 ]. We show how to model the Dining Cryptographers protocol in our probabilistic programming language, and verify anonymity using apex. Let us consider the case of three cryptographers, numbered 1, 2, and 3, from the point of view of the first cryptographer; the open program below enacts the protocol. This program has a local variable whopaid that can be set to 2 or 3, to model the appropriate situation. All events meant to be visible to the first cryptographer, i.e., the outcomes of his two adjacent coins, as well as the announcements of all cryptographers, are written to the free identifiers cn and ch respectively. (Probabilistic) anonymity with respect to the first cryptographer corresponds to the assertion that the program in which whopaid has been set to 2 is equivalent to the program in which whopaid has been set to 3.

void main(var%2 ch, var%2 cn) {
  int%4 whopaid; int%2 first; int%2 right; int%2 left; int%4 i;
  whopaid:=2; first:=coin; right:=first; i:=1;
  while (i) do {
   left := if (i=3) then first else coin;
   if (i=1) then { cn:=right; cn:=left };
   if ((left=right)+(i=whopaid)) then ch:=1 else ch:=0;
   right:=left;
   i:=i+1
  }
 }

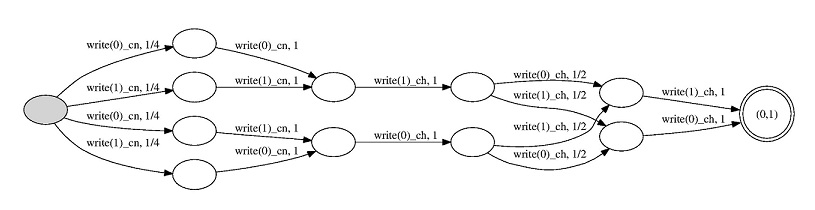
It turns out that setting whopaid to 3 in the above program yields precisely the same automaton. The two programs are therefore equivalent, which establishes anonymity of the protocol with three cryptographers.

One can easily investigate larger instances of the protocol, through very minor modifications of the code. For example, the probabilistic automaton below corresponds to an instance of the protocol comprising 10 cryptographers. It is interesting to note that the size of the state space of the automata grows only linearly with the number of cryptographers, despite the fact that the raw cryptographers state space is ostensibly exponential (due to the set of possible outcomes of the coin flips). Note however that this complexity is in our case reflected in the number of paths of the automata rather than in the number of their states. In fact, in our experiments (see Figure 1), the state spaces of the intermediate automata as well as the total running times grew linearly as well. This unexpected outcome arose partly from apex’s use of bisimulation reduction throughout the construction, in which most symmetries were factored out.

We can also show that probabilistic anonymity fails when the coins are biased, as described in [ Legay et al. ]. Note that thanks to full abstraction, whenever two probabilistic programs are not equivalent, their corresponding probabilistic automata will disagree on the probability of accepting some particular word. This word, whose length need at most be linear in the sizes of the automata, can be thought of as a counterexample to the assertion of equivalence of the original programs, and can potentially be used to ‘debug’ them. In the case at hand, such a word would illustrate why anonymity fails when the coins are biased, albeit only in a probabilistic sense. A would-be spymaster could then return to the programs and attempt to fix the problem.

Although apex does not at present generate counterexamples in instances of inequivalence, we remark that it would be straightforward and computationally inexpensive to instrument it to do so.